Diseño factorial
En estadística, un experimento factorial es un procedimiento de diseño experimental en el que dos o más factores (variables independientes) son tratados de forma simultánea para diferentes valores, generalmente discretos, comprendidos ente un máximo y un mínimo, denominados niveles, de forma que en cada ensayo completo o réplica del experimento se investigan todas las combinaciones posibles de los niveles de los factores, lo que hace que este tipo de diseños sean muy eficientes, desde el punto de vista estadístico.[1] Este tipo de experimentos permiten estudiar el efecto que tiene cada factor sobre la respuesta experimental o variable respuesta, así como el efecto de las interacciones entre factores sobre dicha variable.
Introducción
Los diseños factoriales ya fueron utilizados en el siglo XIX por John Bennet Lawes y Henry J. Gilbert, fundadores, en 1843 de la Estación experimental de Rothamsted, el primer instituto organizado de investigación agrícola del mundo. Gilbert, químico, aportó el rigor científico en la experimentación y estudio de los datos obtenidos de los diferentes experimentos, creando un legado perdurable para la ciencia agrícola,[2] aunque es posible que el término "factorial" no haya sido utilizado como tal, para definir este tipo de diseño experimental, al menos en forma impresa, hasta 1935, cuando R. Fisher lo utilizó en su libro The Design of Experiments (1935).[3] Durante la década de 1920 y comienzo de la de 1930, el biólogo y estadístico inglés Ronald Fisher fue el responsable del análisis de datos y estudio estadístico de la Rothamsted Agricultural Experimental Station. Este científico, en sus discusiones y exposiciones, hacia 1926 ya planteó que los diseños «complejos», tales como los diseños factoriales, eran más eficientes que los estudios unifactoriales, es decir aquellos estudios en los solo se examina un factor cada vez. Fisher escribió: «ningún aforismo se repite tan frecuentemente respecto de las pruebas de campo, que aquel de que a la Naturaleza debemos hacerle pocas preguntas, o, idealmente, hacérselas de a una. Quien escribe está convencido de que este punto de vista está totalmente equivocado».
Los diseños factoriales se consideran muy eficientes, sobre todo en los inicios de un estudio experimental, cuando todavía no se conocen bien cuáles son los factores más influyentes, sus rangos de influencia y sus interacciones. Otro beneficio de estos diseños, es que permiten realizar experimentos en todo el espectro de factores.[4] Por último, un diseño factorial permite que el efecto de varios factores e incluso las interacciones entre ellos sean determinados con el mismo número de ensayos que son necesarios para determinar cualquiera de los efectos por sí solo con el mismo grado de exactitud.
Notación
Los diseños factoriales se describen mediante dos elementos: el número de factores y el número de niveles de cada factor y los experimentos y las condiciones en que se realiza cada cada uno de ellos se obtienen de la combinación, o más correctamente, variación simultánea de todos los factores para cada uno de los de niveles. Por lo tanto, el número total de experimentos que deberán llevarse a cabo con este tipo de diseño se puede establecer de antemano, ya que matemáticamente se tratan de variaciones con repetición.
Donde N indica el número total de experimentos en función de los niveles, l, elegidos y de los factores, k, incluidos en el experimento. De esta manera, en el caso de diseño factorial más sencillo, el de dos factores y dos niveles en cada factor (diseño factorial de 2×2) es necesario realizar 4 experimentos. Para tres factores y dos niveles por factor, el número de experimentos será igual a 8 (23) o si fuera para igual número de factores pero tres niveles, la cantidad total de experimentos a realizar sería N=33; es decir 27 y así sucesivamente.
En los diseños experimentales, sobre todo en los factoriales, es frecuente codificar tanto los factores, como los niveles en los que estos van a variar. Esto se hace por pura comodidad, para ahorrar espacio, sobre todo cuando los nombres de los factores son relativamente largos o complejos y los valores de los niveles, números grandes o con varios decimales, lo que dificulta su escritura. También es habitual escalar los valores de los niveles. El escalado consiste en hacer una transformación matemática de los valores de las variables o factores para que todos ellos queden confinados en un rango [a, b], típicamente [-1, 1]. A veces, cuando con el diseño experimental se busca encontrar qué factores tienen mayor influencia sobre la respuesta experimental, también se suele llevar a cabo una normalización. La normalización consiste en transformar los factores de forma que todos compartan un mismo valor medio y una misma desviación media.
Existen diversas tradiciones para denotar los niveles de cada factor. En este sentido, un diseño factorial que fuera de dos factores para dos niveles de variabilidad de cada factor, los factores podrían codificarse, por ejemplo, como factor A y factor B o, también, factor x1 y factor x2, o de cualquier otra forma que se crea oportuna. En cuanto a los niveles, si van a ser dos y van a estar escalados, el nivel más bajo de cada factor recibe la notación -1 y el más alto +1. También existen otras notaciones utilizadas en diseños de dos niveles, como por ejemplo, denominar el nivel más bajo con el valor 0 y el nivel mas alto con el valor 1. Otra notación, cuando los factores se han codificado con letras mayúsculas, es indicar con la misma letra que el factor, pero en minúscula, el experimento del diseño en que dicho factor se encuentra en el nivel máximo, dando por hecho que el otro se encuentra en su nivel mínimo. Cuando ambos factores se encuentran en el nivel máximo, el experimento se indica con ambas letras y cuando coincide con la combinación en que todos los factores se encuentran en el nivel mínimo, el experimento se codifica con 1.[5] La siguiente tabla muestra diferentes notaciones para un diseño factorial N = 22 (dos factores y dos niveles por factor)
| Experimento | Factor | Combinación | Factor | ||
|---|---|---|---|---|---|
| A (x1) | B (x2) | A (x1) | B (x2) | ||
| 1 | - | - | 1 | 0 | 0 |
| 2 | + | - | a | 1 | 0 |
| 3 | - | + | b | 0 | 1 |
| 4 | + | + | ab | 1 | 1 |
Ejemplo
El experimento factorial más simple contiene dos niveles para cada uno de los factores. Supóngase que un ingeniero desea estudiar la energía total usada por cada uno de dos diferentes motores, A y B, funcionando cada uno en alguna de las siguientes dos velocidades: 2000 o 3000 RPM. El experimento factorial consistiría en los siguientes cuatro elementos experimentales:
| Experimento | Factor (codificado) | Factor (no codificado) | ||
|---|---|---|---|---|
| A | B | Motor A | Motor B | |
| 1 | - | - | 2000 RPM | 2000 RPM |
| 2 | + | - | 3000 RPM | 2000 RPM |
| 3 | - | + | 2000 RPM | 3000 RPM |
| 4 | + | + | 3000 RPM | 3000 RPM |
Como puede verse, nunca se repite la misma combinación de factores y niveles.
Representación gráfica
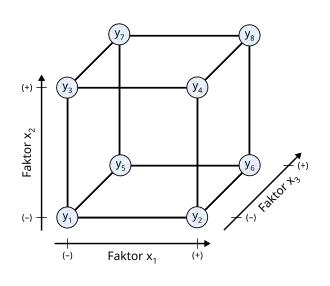
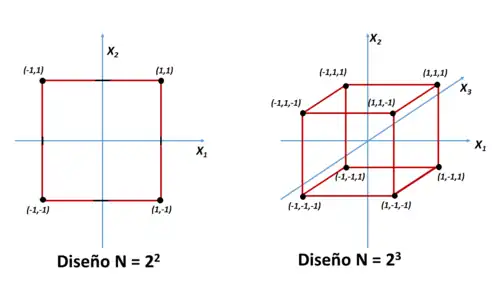
Cuando el número de factores es de dos o de tres y no hay un número elevado de niveles, los diseños pueden ser representados gráficamente mediante figuras geométricas cuyo centro es el centro de coordenadas de un sistema de coordenadas cartesianas en las que cada eje representa un factor. En estos casos es frecuente, aunque no siempre, codificar los factores como x1, x2 y x3 y cada experimento viene representado por las coordenadas de los puntos más significativos. Para facilitar su representación se suelen utilizar los niveles escalados y centrados. Esto permite visualizar rápidamente el diseño y suele ser útil a la hora de la interpretación de las respuestas, ya que es frecuente que cuando el diseño está dirigido al estudio de las respuestas experimentales, los resultados de las medidas correspondientes a cada experimento (variable experimental o dependiente), se coloquen junto a cada vértice, de forma que de una sola mirada se puede apreciar el resultado que tiene cada combinación de niveles y factores sobre el resultado de los experimentos.
En los casos de los diseños de más de dos niveles, también es posible representarlos gráficamente, aunque a medida que aumenta el número de niveles la representación gráfica se hace más compleja. El diseño gráfico para dos factores y tres niveles (N = 32), los nueve posibles experimentos se obtendrían a partir de las coordenadas de los vértices, como en el diseño 2x2, a las que hay que añadir las cuatro coordenadas correspondientes al centro de cada lado del cuadrado más las coordenadas del centro de la figura geométrica. En el caso de un diseño para tres factores y tres niveles, a las coordenadas de los vértices del cubo (8) hay que añadir las correspondientes a los centros de cada arista (12), las de los centros de cada cara (6) y las coordenadas del centro del cubo, en total, veintisiete experimentos (N = 33).
Análisis de Yates
La técnica fundamental consiste en repartir el total en componentes mediante sumas de cuadrados. Esta técnica tuvo efectos secundarios en el modelo. Por ejemplo, demostramos el modelo para un ANOVA simplificado con un tipo de tratamiento en diversos niveles.
Los grados de libertad se pueden repartir de manera similar y especifican distribuciones chi-cuadrado que describen las sumas asociadas de cuadrados.
Prueba F de Fisher
Se utiliza para las comparaciones de los componentes de la desviación total. Por ejemplo, en una forma, o el solo-factor ANOVA, la significación estadística es probada para comparando la estadística de la prueba de F
donde:
- Número de tratamientos: , I
- Total de casos: , nT'
a distribución F con el del I-1, secundario< del > n< T> /sub grados de libertad. Usar la F-distribución es un candidato natural porque la estadística de la prueba es el cociente de dos sumas malas de los cuadrados que tienen a distribución .
Véase también
Referencias
- ↑ Montgomery, Douglas C. (2001). «Chap. 5. Introduction to factorial desig». Design and analysis of experiments (en inglés) (5th ed edición). John Wiley. ISBN 978-0-471-31649-7.
- ↑ Lawes, Sir Joseph Henry Gilbert, John Bennet; Gilbert, Joseph Henry (1895). The Rothamsted Experiments: Being an Account of Some of the Results of the Agricultural Investigations Conducted at Rothamsted (en inglés). Blackwood. Consultado el 01-09-2025.
- ↑ Fisher, R. A. (1935). The Design of Experiments (en inglés). Oliver and Boyd.
- ↑ Otto, Matthias (2017). «Chap. 4.3. Experimental Design and Response Surface Methods». Chemometrics: statistics and computer application in analytical chemistry (en inglés) (Third edition edición). Wiley-VCH. ISBN 978-3-527-34097-2.
- ↑ Morgan, Ed (1991). «Chap. 3.2. Factorial experiments at two leveles». Chemometrics: experimental design. Analytical chemistry by open learning (en inglés). J. Wiley & sons. ISBN 978-0-471-92903-1.