Método de Newton en optimización

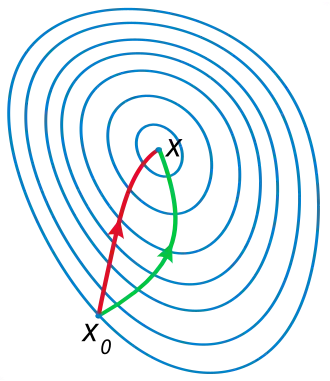
En cálculo infinitesimal, el método de Newton (también llamado de Newton-Raphson) es un procedimiento iterativo para hallar las raíces de una función diferenciable ${\displaystyle f}$, que son soluciones de la ecuación ${\displaystyle f(x)=0}$. Sin embargo, para optimizar una función ${\displaystyle f}$ dos veces diferenciable, el objetivo es hallar las raíces de ${\displaystyle f'}$. Por lo tanto, se puede utilizar el método de Newton en su derivada ${\displaystyle f'}$ para hallar soluciones de ${\displaystyle f'(x)=0}$, también conocidas como los puntos críticos de ${\displaystyle f}$. Estas soluciones pueden ser mínimos, máximos o puntos de inflexión (véase puntos críticos y también la sección "Interpretación geométrica" en este artículo). Esta forma de hallar las raíces de una función es relevante en optimización, cuyo objetivo es hallar los mínimos (globales) de la función ${\displaystyle f}$.

El problema central de la optimización es la minimización de funciones. Considérese primero el caso de las funciones de una sola variable real. Más adelante se abordará el caso de múltiples variables, más general y de mayor utilidad práctica.

Dada una función ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ dos veces diferenciable, se busca resolver el problema de optimización.

${\displaystyle \min _{x\in \mathbb {R} }f(x).}$

El método de Newton intenta resolver este problema construyendo una sucesión ${\displaystyle \{x_{k}\}}$ a partir de un valor inicial (punto de partida) ${\displaystyle x_{0}\in \mathbb {R} }$ que converge hacia un minimizador ${\displaystyle x_{*}}$ de ${\displaystyle f}$ mediante una secuencia de aproximaciones de Taylor de segundo orden de ${\displaystyle f}$ en torno a las iteraciones. La serie de Taylor de segundo orden de f en torno a ${\displaystyle x_{k}}$ es

${\displaystyle f(x_{k}+t)\approx f(x_{k})+f'(x_{k})t+{\frac {1}{2}}f''(x_{k})t^{2}.}$

La siguiente iteración, ${\displaystyle x_{k+1}}$, se define de forma que minimice esta aproximación cuadrática en ${\displaystyle t}$ y establezca ${\displaystyle x_{k+1}=x_{k}+t}$. Si la segunda derivada es positiva, la aproximación cuadrática es una función convexa de ${\displaystyle t}$, y su mínimo se puede obtener estableciendo la derivada en cero. Dado que

${\displaystyle \displaystyle 0={\frac {\rm {d}}{{\rm {d}}t}}\left(f(x_{k})+f'(x_{k})t+{\frac {1}{2}}f''(x_{k})t^{2}\right)=f'(x_{k})+f''(x_{k})t,}$

se alcanza el mínimo para

${\displaystyle t=-{\frac {f'(x_{k})}{f''(x_{k})}}.}$

En resumen, el método de Newton realiza la iteración

${\displaystyle x_{k+1}=x_{k}+t=x_{k}-{\frac {f'(x_{k})}{f''(x_{k})}}.}$

La interpretación geométrica del método de Newton es que, en cada iteración, equivale a ajustar una función parabólica a la función gráfica de ${\displaystyle f(x)}$ en el valor de prueba ${\displaystyle x_{k}}$, con la misma pendiente y curvatura que la gráfica en ese punto, y luego proceder al máximo o mínimo de dicha parábola (en dimensiones superiores, esto también puede ser una función con un punto de silla), véase más adelante. Nótese que si ${\displaystyle f}$ resulta ser una función cuadrática, entonces el punto extremo exacto buscado se encuentra en un solo paso.

El esquema iterativo anterior se puede generalizar a dimensiones ${\displaystyle d>1}$ reemplazando la derivada por el gradiente (diferentes autores utilizan diferentes notaciones para el gradiente, incluyendo ${\displaystyle f'(x)=\nabla f(x)=g_{f}(x)\in \mathbb {R} ^{d}}$), y el recíproco de la segunda derivada por la inversa de la matriz hessiana (diferentes autores utilizan distintas notaciones para el hessiano, incluyendo ${\displaystyle f''(x)=\nabla ^{2}f(x)=H_{f}(x)\in \mathbb {R} ^{d\times d}}$). De este modo, se obtiene el esquema iterativo:

${\displaystyle x_{k+1}=x_{k}-[f''(x_{k})]^{-1}f'(x_{k}),\qquad k\geq 0.}$

Con frecuencia, el método de Newton se modifica para incluir un tamaño del paso pequeño en lugar de ${\displaystyle 0<\gamma \leq 1}$:

${\displaystyle \gamma =1}$

${\displaystyle x_{k+1}=x_{k}-\gamma [f''(x_{k})]^{-1}f'(x_{k}).}$

Esto se hace a menudo para garantizar que las condiciones de Wolfe, o una condición de Armijo mucho más simple y eficiente, se satisfagan en cada paso del método. Para tamaños de paso distintos de 1, el método se suele denominar método de Newton relajado o amortiguado.

Si f es una función fuertemente convexa con hessiano de Lipschitz, siempre que ${\displaystyle x_{0}}$ sea lo suficientemente cercana a ${\displaystyle x_{*}=\arg \min f(x)}$, la secuencia ${\displaystyle x_{0},x_{1},x_{2},\dots }$ generada por el método de Newton convergerá al minimizador (necesariamente único) ${\displaystyle x_{*}}$ de ${\displaystyle f}$ con una velocidad cuadrática.^[1]​ Es decir,

${\displaystyle \|x_{k+1}-x_{*}\|\leq {\frac {1}{2}}\|x_{k}-x_{*}\|^{2},\qquad \forall k\geq 0.}$

Encontrar la inversa del hessiano en grandes dimensiones para calcular la dirección de Newton ${\displaystyle h=-(f''(x_{k}))^{-1}f'(x_{k})}$ puede ser una operación costosa. En tales casos, en lugar de invertir directamente el hessiano, es mejor calcular el vector ${\displaystyle h}$ como solución del sistema de ecuaciones lineales

${\displaystyle [f''(x_{k})]h=-f'(x_{k})}$

que puede resolverse mediante diversas factorizaciones o de forma aproximada (pero con gran precisión) utilizando un método iterativo. Muchos de estos métodos solo son aplicables a ciertos tipos de ecuaciones. Por ejemplo, la factorización de Cholesky y el método del gradiente conjugado solo funcionarán si ${\displaystyle f''(x_{k})}$ es una matriz definida positiva. Aunque esto pueda parecer una limitación, suele ser un indicador útil de que algo ha fallado. Por ejemplo, si se aborda un problema de minimización y ${\displaystyle f''(x_{k})}$ no es definida positiva, las iteraciones convergen a un punto de silla y no a un mínimo.

Por otro lado, si se realiza una optimización con restricciones (por ejemplo, con multiplicadores de Lagrange), el problema puede convertirse en uno de búsqueda de puntos de silla, en cuyo caso la matriz hessiana será simétricamente indefinida y la solución de ${\displaystyle x_{k+1}}$ deberá realizarse con un método adecuado, como la variante ${\displaystyle LDL^{\top }}$ de la factorización de Cholesky o el método del conjugado residual.

También existen varios casi métodos de Newton, donde una aproximación para la matriz hessiana (o su inversa directa) se construye a partir de cambios en el gradiente.

Si la matriz hessiana se acerca a una matriz no invertible, la hessiana invertida puede ser numéricamente inestable y la solución puede divergir. En este caso, se han probado anteriormente ciertas soluciones alternativas, con resultados variables en ciertos problemas. Por ejemplo, se puede modificar la hessiana añadiendo una matriz de corrección ${\displaystyle B_{k}}$ para que ${\displaystyle f''(x_{k})+B_{k}}$ sea definida positiva. Un enfoque consiste en diagonalizar la hessiana y elegir ${\displaystyle B_{k}}$ de modo que ${\displaystyle f''(x_{k})+B_{k}}$ tenga los mismos vectores propios que la hessiana, pero con cada valor propio negativo reemplazado por ${\displaystyle \epsilon >0}$.

Un enfoque explotado en el algoritmo de Levenberg-Marquardt (que utiliza una matriz hessiana aproximada) consiste en añadir una matriz identidad escalada a la hessiana, ${\displaystyle \mu I}$, ajustando la escala en cada iteración según sea necesario. Para ${\displaystyle \mu }$ grandes y hessianas pequeñas, las iteraciones se comportarán como un descenso del gradiente con un tamaño de paso ${\displaystyle 1/\mu }$. Esto resulta en una convergencia más lenta, pero más fiable, donde la hessiana no proporciona información útil.

El método de Newton, en su versión original, tiene varias advertencias:

1. No funciona si la matriz hessiana no es invertible. Esto se desprende de la propia definición del método de Newton, que requiere obtener la inversa de la matriz hessiana.
2. Puede no converger en absoluto, pero puede entrar en un ciclo con más de un punto (véase Análisis de fallos en el método de Newton).
3. Puede converger a un punto de silla en lugar de a un mínimo local.

Las modificaciones populares del método de Newton, como los casi métodos de Newton o el algoritmo de Levenberg-Marquardt mencionados anteriormente, también presentan salvedades:

Por ejemplo, generalmente se requiere que la función de coste sea (fuertemente) convexa y que la hessiana esté globalmente acotada o sea continua en el sentido de Lipschitz. Esto se menciona en la sección "Convergencia" del presente artículo. Si se consultan los artículos de Levenberg y Marquardt en la referencia del Algoritmo de Levenberg-Marquardt, que son las fuentes originales del método mencionado, se puede observar que el artículo de Levenberg carece básicamente de análisis teórico, mientras que el de Marquardt solo analiza una situación local y no demuestra un resultado de convergencia global. Se puede comparar con el método de búsqueda de línea de retroceso para el descenso de gradiente, que ofrece una buena garantía teórica bajo supuestos más generales, y puede usarse y funcionar bien en problemas prácticos a gran escala, como las redes neuronales profundas.

• Método de Newton
• Casi método de Newton
• Descenso del gradiente
• Algoritmo de Gauss-Newton
• Algoritmo de Levenberg-Marquardt
• Región de confianza
• Optimización
• Método Nelder-Mead
• Función autoconcordante, una función para la que el método de Newton presenta una tasa de convergencia global muy buena.^[2]​^: Sec.6.2

• Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0. 
• Bonnans, J. Frédéric; Gilbert, J. Charles; Lemaréchal, Claude; Sagastizábal, Claudia A. (2006). Numerical optimization: Theoretical and practical aspects. Universitext (Second revised ed. of translation of 1997 French edición). Berlin: Springer-Verlag. ISBN 3-540-35445-X. MR 2265882. doi:10.1007/978-3-540-35447-5. 
• Fletcher, Roger (1987). Practical Methods of Optimization (2nd edición). New York: John Wiley & Sons. ISBN 978-0-471-91547-8. 
• Givens, Geof H.; Hoeting, Jennifer A. (2013). Computational Statistics. Hoboken, New Jersey: John Wiley & Sons. pp. 24-58. ISBN 978-0-470-53331-4. 
• Nocedal, Jorge; Wright, Stephen J. (1999). Numerical Optimization. Springer-Verlag. ISBN 0-387-98793-2. 
• Kovalev, Dmitry; Mishchenko, Konstantin; Richtárik, Peter (2019). «Stochastic Newton and cubic Newton methods with simple local linear-quadratic rates».

. 

• Korenblum, Daniel (29 de agosto de 2015). «Newton-Raphson visualization (1D)». Bl.ocks. ffe9653768cb80dfc0da.